5月30日，“分布依赖型随机微分方程的正则性（Regularities of Distribution Dependent SDEs）”专题讲座在理学院钱伟长楼201会议室举行，南京大学数学学院宋玉林副教授应邀担任主讲嘉宾。讲座由理学院高洁教授主持，吸引了众多对随机分析、金融数学及泛函分析研究感兴趣的师生前来参加。

宋老师首先介绍了Wasserstein距离的核心概念及其在概率测度空间中的重要性，阐述了依赖分布型随机微分方程的基本形式。随后又详细讨论了带跳跃的此类方程的假设条件，包括对系数函数的光滑性、有界性要求，以及对跳跃测度的刻画条件，这些条件是研究方程解的性质的基础。

在核心理论部分，宋老师讨论了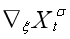的存在性结论以及其满足的方程，为分析解的规律性提供了关键工具。针对依赖分布情形的特殊性，宋老师对比了经典随机微分方程的研究方法，指出传统基于初始值扰动的思路不再适用。为此，他引入了Lions导数的概念，通过具体公式刻画了泛函对概率分布变化的敏感性，并定义了随机微分方程的两个解 J_t 和K_t（初始值均为单位矩阵），通过构造矩阵工具推导关键理论结果（如Bismut公式）。

这一理论在金融领域具有重要应用，例如分析期权价格对市场参数的依赖关系，解决复杂市场环境下金融产品的风险评估难题。宋老师将抽象的数学理论与金融实务紧密结合，以欧式期权定价为例，展示了分布依赖型随机微分方程在金融衍生品领域的应用。他介绍了如何通过随机分析方法结合Bismut公式推导期权价格的导数公式，并通过有限差分法与Malliavin方法数值模拟验证理论结果。现场展示的模拟图像呈现了欧式看涨期权与数字期权的价格变化曲线，直观揭示了不同参数对期权价值的影响规律。同时宋老师也提到在多次实验结果中，通过Malliavin方法得到的图像更具优势。此外，他还拓展介绍了由分数布朗运动驱动的依赖分布随机微分方程，为参会者提供了宝贵的学术指导。

整个讲座内容丰富、条理清晰，历时一个多小时，为参会者带来了一场前沿的学术盛宴。通过此次讲座，不仅加深了师生对分布依赖型随机微分方程正则性理论的理解，还从金融应用和数值计算等多维度拓宽了研究思路，为今后的科研工作提供了重要参考。

宋玉林副教授博士毕业于中国科学院数学与系统科学研究院，研究方向为随机微分方程。目前已在DCDS, JTP, EJP等杂志发表论文多篇，先后主持国家自然科学基金两项，江苏省自然科学基金一项，参与国家自然科学基金重大项目一项。

宋玉林副教授作学术讲座